So the last business week was pretty fucking insane. We had a three-day bull run in the stock market due to the Coronavirus bill being authored by Congress, and then for some reason the stock market crashed again after the bill passed. It’s all over the place, and probably will continue to be that way for at least a few more days, until the novelty of the Coronavirus bill wears off and it starts to go down again simply due to the inertia of business shutdowns and Coronavirus spiraling out of control in the US. Until then, mathematical models of the Coronavirus spread are pretty much useless in predicting the stock market, so I’ll probably have to put the applied part of the Corona-Chan project on hold until then.
But it’s still interesting to continue developing a mathematical theory just for academic purposes, and maybe I can apply this at a later date when the market is less volatile. Specifically I want to start looking at data from the US, because that’s basically the epicenter of Coronavirus spread at the moment, so it’ll be very interesting to look at how it develops over the next couple weeks.
First of all, if you haven’t be sure to go back and read:
Part 1
Part 2
Part 3
In this part of the project I will be fitting the mathematical model of Coronavirus spread – meaning the one based on the hyperbolic tangent function – to the actual Coronavirus data. To do this, I will be operating under the assumption that the Coronavirus data can be approximately modeled by a linear transformation of the hyperbolic tangent function (I defined linear transformations of functions in Part 3 of this series). The function will be of the form y = c*tanh(ax–b)+d, so basically our goal is to find the parameters a and b that transform the x coordinates and the parameters c and d that transform the y coordinates. These will completely determine our function.
First let’s look at how we would do this if we had all of the data available. Let’s say we were doing this a year from now when Coronavirus is long gone and we have all the data points we need. We’re no longer predicting anything, we’re just taking the data and fitting a mathematical function to that data. The standard method of doing this is logistic regression (so called because it uses the logistic function, which is another sigmoid curve). This is a statistical method often used in classification problems in machine learning, and it basically consists of finding where the inflection point of the data is – that is, where the data goes from being mostly below the threshold to being mostly above the threshold – and plotting a sigmoid function whose inflection point is at that point. We can modify this method slightly to allow us to solve a problem dealing with multiple parameters. The principle is the same – figure out where the critical points of the data are and plot curves with those same critical points.
The functions we’re looking for, with their parameters, are as follows:
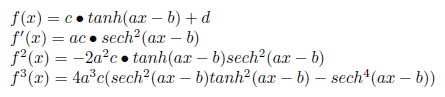
Theoretically, because we have four parameters to solve for, we will need four equations to uniquely determine those parameters. The equations are obtained by setting the derivative functions to zero and plugging in the value of x at those critical points. Obviously we won’t be able to get d this way since it is only present in the first equation, which is never zero (we can add it in later using other means). This means we will need three equations to solve for a, b, and c. These can be obtained by taking the one zero point of the second derivative and the two zero points of the third derivative.

These equations can be simplified to:

Notice that we’ve now eliminated c from this system of equations. It turns out the parameters that transform the y coordinates cannot be obtained from these equations. What we need is way find the parameters that transform the x coordinates, and then once we have them, we can use some simple comparisons between the equations and the data points to find values for c and d that translate and scale the graphs so that they approximately coincide with the data.
With this in mind, we really only need two equations, and this makes our job a lot easier when we only have an early section of the data. If the only zero point we have is the zero point for the third derivative, then we now have to consult the fourth derivative for a critical point that is within our range. Luckily, since we are only solving for two parameters, this is as far as we have to go. Of course if we only have the maximum for the third derivative, we will have to take the fourth and fifth derivatives, but for simplicity’s sake, we will assume we have the zero point (if we don’t, the method I’m about to develop still works just as well).

Our first instinct might be to try to isolate one of the variables, solve for the other, and then solve for the first like we would do in elementary algebra. However, if you do this, you’ll quickly find yourself stumped by the sheer complexity of the equations. You can go ahead and try to solve them; they’re pretty much impossible. There’s no way that I can see to isolate either a or b in the above system of equations.
So we need an alternative method. Instead of solving the problem analytically we will have to solve the problem numerically. We can do this by essentially sampling large numbers of ordered pairs (a,b) and seeing which ones result in values very close to zero. To do this, we will set z equal to the left sides of the equations to get two surfaces and then plot the curves formed by the respective intersections of the two surfaces with the ab-plane.
The flowchart for the program to implement the aforementioned process looks like this:
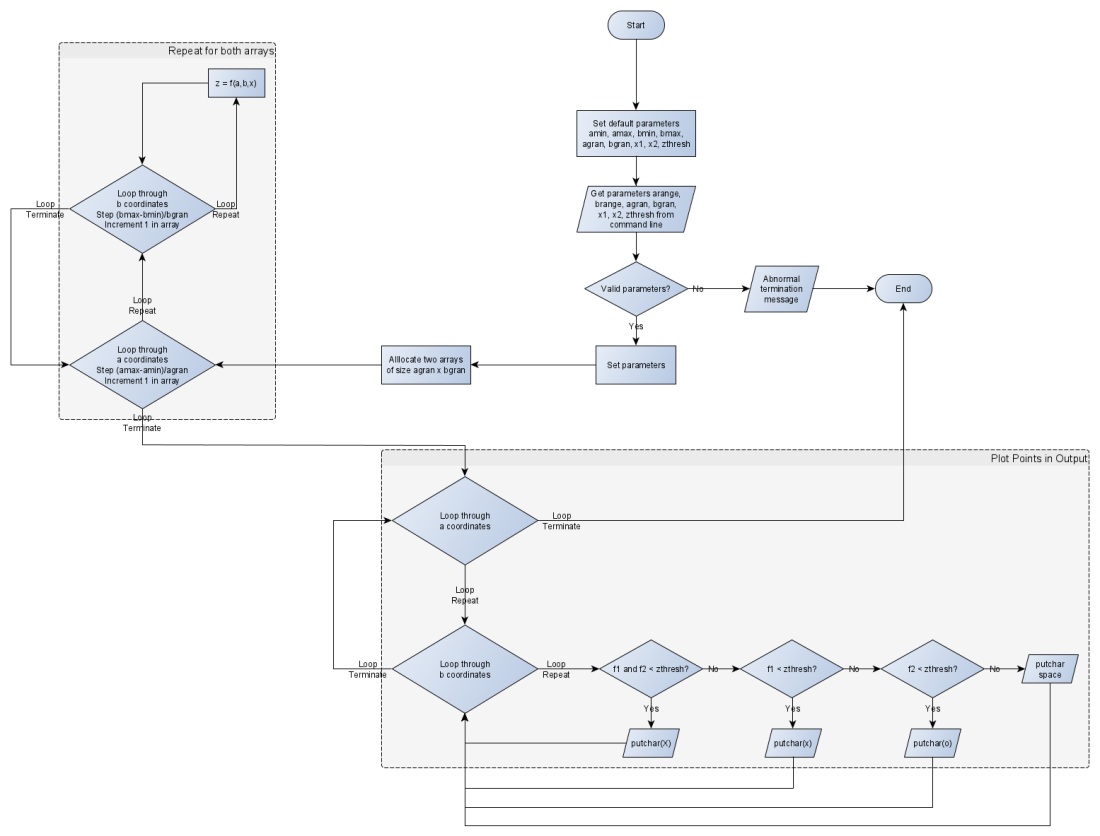
The first finished version of the source code for the program looks like this:
1 #include <stdio.h>
2 #include <stdlib.h>
3 #include <string.h>
4 #include <math.h>
5 #include <stdbool.h>
6
7 float amin = -10; // Must be < amax
8 float amax = 10; // Must be > amin
9 float bmin = -10; // Must be < bmax
10 float bmax = 10; // Must be > amin
11 unsigned int agran = 79; // Must be nonzero
12 unsigned int bgran = 79; // Must be nonzero
13 float x1; // Must be entered and must be > x2
14 float x2; // Must be entered and must be < x1
15 float zthresh = 1; // Must be non-negative
16
17 #define sech( x ) (1/cosh(x))
18
19 // Third derivative
20 #define f1( a, b, x1 )\
21 (pow( sech( a*x1-b), 2 ) * pow( tanh( a*x1-b ), 2 ) - pow( sech( a*x1 - b ), 4 ))
22
23 // Fourth derivative
24 #define f2( a, b, x2 )\
25 (3 * tanh( a*x2-b ) * pow( sech( a*x2-b ), 4 ) - pow( tanh( a*x2-b ), 3 ) * pow( sech( a*x2-b ), 2 ))
26
27 void main( int argc, char **argv ){
28 float **grid1; // Grid for plotting f1
29 float **grid2; // Grid for plotting f2
30 float a, b; // Independent variables
31 float ainc, binc; // Increments for a and b
32 int i, j; // Loop counters
33 int len; // Holds result of strlen()
34 char *buf; // Buffer for parsing strings
35 char *key; // Key in key=value pair
36 char *value; // Value in key=value pair
37 bool _x1 = false; // x1 is required argument
38 bool _x2 = false; // x2 is required argument
39 int eqlcount = 0; // Number of = in argument
40 // Begin parse command line arguments
41 for( i = 1; i < argc; i++ ){
42 len = strlen( argv[i] );
43 buf = (char *) malloc( len + 1 );
44 strcpy( buf, argv[i] );
45 buf[len] = '\0';
46 for( j = 0; j < len; j++ ){
47 if( buf[j] == '=' ) eqlcount++;
48 }
49 if( eqlcount != 1 ) goto __invalid_argument_error;
50 eqlcount = 0;
51 key = strtok( buf, "=" );
52 value = strtok( NULL, "\0" );
53 if( !strcmp( key, "zthresh" ) ){
54 zthresh = atof( value );
55 if( zthresh < 0 ) goto __invalid_argument_error;
56 }
57 else if( !strcmp( key, "x1" ) ){
58 _x1 = true;
59 x1 = atof( value );
60 }
61 else if( !strcmp( key, "x2" ) ){
62 _x2 = true;
63 x2 = atof( value );
64 }
65 else if( !strcmp( key, "agran" ) ){
66 agran = atoi( value );
67 if( !agran ) goto __invalid_argument_error;
68 }
69 else if( !strcmp( key, "bgran" ) ){
70 bgran = atoi( value );
71 if( !bgran ) goto __invalid_argument_error;
72 }
73 else if( !strcmp( key, "arange" ) ){
74 len = strlen( value );
75 if( value[0] != '(' || value[len-1] != ')' ) goto __invalid_argument_error;
76 amin = atof( strtok( value+1, "," ) );
77 amax = atof( strtok( NULL, ")" ) );
78 if( amax <= amin ) goto __invalid_argument_error;
79 }
80 else if( !strcmp( key, "brange" ) ){
81 len = strlen( value );
82 if( value[0] != '(' || value[len-1] != ')' ) goto __invalid_argument_error;
83 bmin = atof( strtok( value+1, "," ) );
84 bmax = atof( strtok( NULL, ")" ) );
85 if( bmax <= bmin ) goto __invalid_argument_error;
86 }
87 else goto __invalid_argument_error;
88 }
89 if( !_x1 || !_x2 ) goto __invalid_argument_error;
90 if( x1 <= x2 ) goto __invalid_argument_error;
91 goto __no_error;
92 __invalid_argument_error:
93 fprintf( stderr, "%s: Invalid argument(s)\n", argv[0] );
94 fprintf( stderr, "Usage: fitmodel x1=_ x2=_ arange=(_,_) brange=(_,_) agran=_ bgran=_ zthresh=_\n" );
95 fprintf( stderr, "x1 and x2 are required, other parameters are optional\n" );
96 fprintf( stderr, "Also required: x1 > x2, range=(lower,higher), gran > 0, zthresh > 0\n" );
97 exit( -1 );
98 __no_error:
99 // End parse command line arguments
100 printf( "x1=%.3f\nx2=%.3f\narange=(%.3f,%.3f)\nbrange=(%.3f,%.3f)\nagran=%i\nbgran=%i\nzthresh=%.3f\n",
101 x1, x2, amin, amax, bmin, bmax, agran, bgran, zthresh );
102 // Allocate arrays:
103 grid1 = (float **) malloc( sizeof( float * ) * agran );
104 for( i = 0; i < agran; i++ ){
105 grid1[i] = (float *) malloc( sizeof( float ) * bgran );
106 }
107 grid2 = (float **) malloc( sizeof( float * ) * agran );
108 for( i = 0; i < agran; i++ ){
109 grid2[i] = (float *) malloc( sizeof( float ) * bgran );
110 }
111 // Populate arrays:
112 ainc = (amax-amin)/agran;
113 binc = (bmax-bmin)/bgran;
114 a = amin;
115 for( i = 0; i < agran; i++ ){
116 a += ainc;
117 b = bmin;
118 for( j = 0; j < bgran; j++ ){
119 b += binc;
120 grid1[i][j] = f1( a, b, x1 );
121 grid2[i][j] = f2( a, b, x2 );
122 }
123 }
124 // Plot points:
125 for( i = 0; i < agran; i++ ){
126 for( j = 0; j < bgran; j++ ){
127 if( fabs( grid1[i][j] ) < zthresh && fabs( grid2[i][j] ) < zthresh ){
128 putchar( '0' );
129 }
130 else if( fabs( grid1[i][j] ) < zthresh ){
131 putchar( 'x' );
132 }
133 else if( fabs( grid2[i][j] ) < zthresh ){
134 putchar( 'o' );
135 }
136 else putchar( '.' );
137 }
138 putchar( '\n' );
139 }
140 }
Here is a sample output from this program, using the completely arbitrary values 2 and 1 for x1 and x2 respectively:

I’m not sure if this is in any way correct. I may have messed up on some part, so I’ll have to go back and check the code to see. But assuming it is correct, it looks promising, because we can see a diagonal line down the middle where the fourth derivative is zero. This gives us a linear relationship between a and b, which may make a precise calculation of their correct values a lot easier. I will have to do some more research on this to see. Until then, happy hacking, and don’t let Corona-Chan get you!
